Javascript数据结构之树、二叉树

树

树是一种分层数据的抽象模型。

一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点（除了顶部的第一个节点）以及零个或多个子节点。

• 二叉树和二叉树搜索

二叉树中的节点最多只能有两个子节点：一个左侧子节点，另一个是右侧子节点。

二叉树搜索（BST）是二叉树的一种，但是只允许你在左侧节点存储比父节点小的值，在右侧节点存储比父节点大的值。

BinarySearchTree类

• insert(key): 向树中插入一个新的键
• search(key): 在树中查找一个键，返回 true/false
• inOrderTraverse(): 通过中序遍历方式遍历所有节点
• preOrderTraverse(): 通过先序遍历方式遍历所有节点
• postOrderTraverse(): 通过后序遍历方式遍历所有节点
• min(): 返回树中最小的值/键
• max(): 返回树中最大的值/键
• remove(key): 从树中移除某个键

const Compare = {
  LESS_THAN: -1,
  BIGGER_THAN: 1,
  EQUALS: 0
};

function defaultCompare(a, b) {
  if (a === b) {
    return Compare.EQUALS;
  }
  return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}

class Node {
  constructor(key) {
    this.key = key;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor(compareFn = defaultCompare) {
    this.compareFn = compareFn;
    this.root = null;
  }

  // 向树中插入一个新的键
  insert(key) {
    if (this.root === null) {
      this.root = new Node(key);
    } else {
      this.insertNode(this.root, key);
    }
  }

  insertNode(node, key) {
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      if (node.left === null) {
        node.left = new Node(key);
      } else {
        this.insertNode(node.left, key);
      }
    } else {
      if (node.right === null) {
        node.right = new Node(key);
      } else {
        this.insertNode(node.right, key);
      }
    }
  }

  getRoot() {
    return this.root;
  }

  // 中序遍历
  inOrderTraverse(callback) {
    this.inOrderTraverseNode(this.root, callback);
  }
  inOrderTraverseNode(node, callback) {
    if (node !== null) {
      this.inOrderTraverseNode(node.left, callback);
      callback(node.key);
      this.inOrderTraverseNode(node.right, callback);
    }
  }

  // 先序遍历
  preOrderTraverse(callback) {
    this.preOrderTraverseNode(this.root, callback);
  }
  preOrderTraverseNode(node, callback) {
    if (node !== null) {
      callback(node.key);
      this.preOrderTraverseNode(node.left, callback);
      this.preOrderTraverseNode(node.right, callback);
    }
  }

  // 后序遍历
  postOrderTraverse(callback) {
    this.postOrderTraverseNode(this.root, callback);
  }
  postOrderTraverseNode(node, callback) {
    if (node !== null) {
      this.postOrderTraverseNode(node.left, callback);
      this.postOrderTraverseNode(node.right, callback);
      callback(node.key);
    }
  }

  // 最小值
  min() {
    return this.minNode(this.root);
  }
  minNode(node) {
    let current = node;
    while(current !== null && current.left !== null) {
      current = current.left;
    }
    return current;
  }

  // 最大值
  max() {
    return this.maxNode(this.root);
  }
  maxNode(node) {
    let current = node;
    while(current !== null && current.right !== null) {
      current = current.right;
    }
    return current;
  }

  // 搜索值
  search(key) {
    return this.searchNode(this.root, key);
  }
  searchNode(node, key) {
    if (node === null) {
      return false;
    }
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      return this.searchNode(node.left, key);
    } else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
      return this.searchNode(node.right, key);
    } else {
      return true;
    }
  }

  // 移除节点
  remove(key) {
    this.root = this.removeNode(this.root, key);
  }
  removeNode(node, key) {
    if (node === null) {
      return null;
    }
    if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      node.left = this.removeNode(node.left, key);
      return node;
    } else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
      node.right = this.removeNode(node.right, key);
      return node;
    } else {
      // 键等于 node.key
      if (node.left === null && node.right === null) {
        node = null;
        return node;
      }
      if (node.left === null) {
        node = node.right;
        return node;
      } else if (node.right === null) {
        node = node.left;
        return node;
      }
      const aux = this.minNode(node.right);
      node.key = aux.key;
      node.right = this.removeNode(node.right, aux.key);
      return node;
    }
  }
}

const tree = new BinarySearchTree();
tree.insert(11);
console.log(tree.getRoot()) // Node { key: 11, left: null, right: null }
tree.insert(7);
tree.insert(15);
tree.insert(5);
tree.insert(3);
tree.insert(9);
tree.insert(8);
tree.insert(10);
tree.insert(13);
tree.insert(12);
tree.insert(14);
tree.insert(20);
tree.insert(18);
tree.insert(25);
const printNode = (value) => console.log(value);
tree.inOrderTraverse(printNode);
console.log('-----------------------------')
tree.preOrderTraverse(printNode);
console.log('-----------------------------')
tree.postOrderTraverse(printNode);
console.log(tree.min()); // Node { key: 3, left: null, right: null }
console.log(tree.max()); // Node { key: 25, left: null, right: null }
console.log(tree.search(10)); // true
console.log(tree.search(100)); // false
console.log(tree.remove(11));
console.log(tree.getRoot())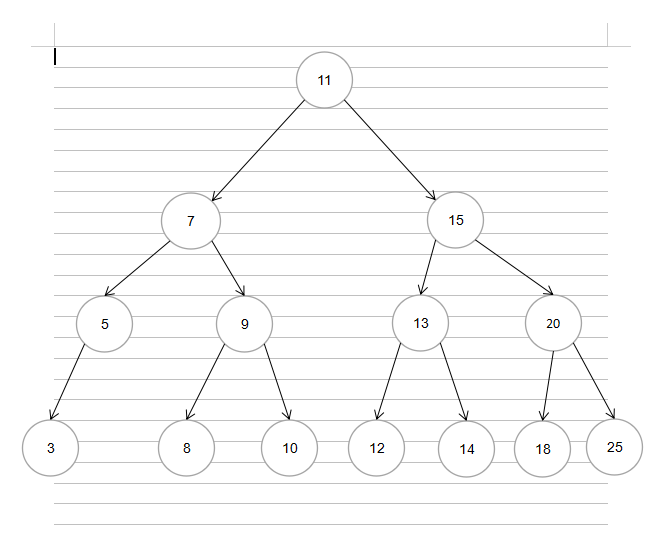

• AVL 树

AVL树是一种自平衡树。添加或移除节点时，AVL树会尝试保持自平衡。任意一个节点不论深度的左子树和右子树高度最多相差1。添加或移除节点时，AVL树会尽可能尝试转换为完全树。

const BalanceFactor = {
  UNBALANCED_RIGHT: 1,
  SLIGHTLY_UNBALANCED_RIGHT: 2,
  BALANCED: 3,
  SLIGHTLY_UNBALANCED_LEFT: 4,
  UNBALANCED_LEFT: 5
};

class AVLTree extends BinarySearchTree {
  constructor(compareFn = defaultCompare) {
    super(compareFn);
    this.compareFn = compareFn;
    this.root = null;
  }

  // 获取节点最大高度
  getNodeHeight(node) {
    if (node === null) {
      return -1;
    }
    return Math.max(this.getNodeHeight(node.left), this.getNodeHeight(node.right)) + 1;
  }

  // 计算树的平衡因子
  getBalanceFactor(node) {
    const heightDifference = this.getNodeHeight(node.left) - this.getNodeHeight(node.right);
    switch(heightDifference) {
      case -2:
        return BalanceFactor.UNBALANCED_RIGHT;
      case -1:
        return BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT;
      case 1:
        return BalanceFactor.SLIGHTLY_UNBALANCED_LEFT;
      case 2:
        return BalanceFactor.UNBALANCED_LEFT;
      default:
        return BalanceFactor.BALANCED;       
    }
  }

  // 左-左（LL）：向右的单旋转
  rotationLL(node) {
    const tmp = node.left;
    node.left = tmp.right;
    tmp.right = node;
    return tmp;
  }

  // 右-右（RR）：向左的单旋转
  rotationRR(node) {
    const tmp = node.right;
    node.right = tmp.left;
    tmp.left = node;
    return tmp;
  }

  // 左-右（LR）：向右的双旋转
  rotationLR(node) {
    node.left = this.rotationRR(node.left);
    return this.rotationLL(node);
  }

  // 右-左（RL）：向左的双旋转
  rotationRL(node) {
    node.right = this.rotationLL(node.right);
    return this.rotationRR(node);
  }

  // 插入节点
  insert(key) {
    this.root = this.insertNode(this.root, key);
  }
  insertNode(node, key) {
    if (node === null) {
      return new Node(key);
    } else if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
      node.left = this.insertNode(node.left, key);
    } else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {
      node.right = this.insertNode(node.right, key);
    } else {
      return node;
    }
    
    // 如果需要，将树进行平衡操作
    const balanceFactor = this.getBalanceFactor(node);
    if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
      if (this.compareFn(key, node.left.key) === Compare.LESS_THAN) {
        node = this.rotationLL(node);
      } else {
        return this.rotationLR(node);
      }
    }
    if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
      if (this.compareFn(key, node.right.key) === Compare.BIGGER_THAN) {
        node = this.rotationRR(node);
      } else {
        return this.rotationRL(node);
      }
    }
    return node;
  }

  // 从AVL树中移除节点
  removeNode(node, key) {
    node = super.removeNode(node, key);
    if (node === null) {
      return node;
    }

    // 检查树是否平衡
    const balanceFactor = this.getBalanceFactor(node);
    if (balanceFactor === BalanceFactor.UNBALANCED_LEFT) {
      const balanceFactorLeft = this.getBalanceFactor(node.left);
      if (
        balanceFactorLeft === BalanceFactor.BALANCED ||
        balanceFactorLeft === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT
      ) {
        return this.rotationLL(node);
      }
      if (
        balanceFactorLeft = BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT
      ) {
        return this.rotationLR(node.left);
      }
    }
    if (balanceFactor === BalanceFactor.UNBALANCED_RIGHT) {
      const balanceFactorRight = this.getBalanceFactor(node.right);
      if (
        balanceFactorRight === BalanceFactor.BALANCED ||
        balanceFactorRight === BalanceFactor.SLIGHTLY_UNBALANCED_RIGHT
      ) {
        return this.rotationRR(node);
      }
      if (
        balanceFactorRight === BalanceFactor.SLIGHTLY_UNBALANCED_LEFT
      ) {
        return this.rotationRL(node.right);
      }
    }
    return node;
  }
}